[Sampling] 중요도 샘플링 (Importance Sampling: IS)

1. Importance Sampling

• 정의
  • 효율적으로 기댓값을 추정하기 위해 고안되었으며, 확률 밀도 추정 및 강화 학습 등의 다양한 활용에 이용
  • 기댓값을 계산하고자 하는 확률 분포 p(x)의 확률 밀도 함수 (probability density function, PDF)를 알고는 있지만 p에서 샘플을 생성하기가 어려울 때, 비교적 샘플을 생성하기가 쉬운 q(x)에서 샘플을 생성하여 p 의 기댓값을 계산하는 것
  • 즉, pdf(p(x))로 임의의 샘플을 생성하지 않음. Monte Carlo sampling 정확도를 향상시키기 위해 왜곡된 pdf(q(x))를 찾는다.

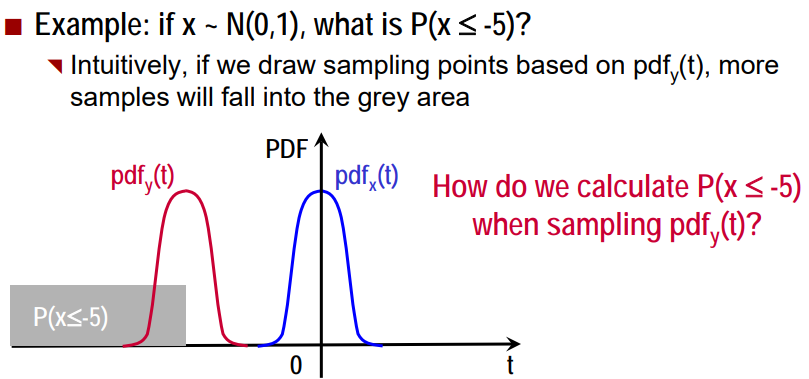
• 활용 예
  • 어휘량이 많은 neural language models의 학습을 가속화하기 위해
  • Estimate partition function (분할 함수 추정: normalize prob. distribution)
  • Estimate log-likelihood in deep directed models such as variational autoencoder
  • Estimate gradient in SGD where most of the cost comes from a small no of misclassified samples

 

2. Process

1) pdf_y(t)를 기반으로 M개의 임의의 샘플 추출(t1, t2, ..., tM)

2) 각 샘플링 점 m = 1, 2, ..., M에서의 g_m 계산

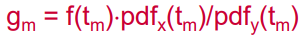
3) E[f] ~~ (g1+g2+...+gM)/M 계산

 

그럼 어떻게 최적의 pdf_y(f)를 결정할까?

추정의 정확도는 분산에 의해 정량적으로 측정될 수 있고, 이 분산을 줄여야 한다.

 

k는 임의로 선택할 수 없다.

 

실제 환경에서는, 최적의 pdf를 쉽게 적용할 수 없다.

대신, sub-optimal solution을 찾는다.

• easy to construct : k=E[f]를 알 필요가 없다.
• easy to sample : 모든 랜덤 분포가 랜덤 수 생성으로 쉽게 샘플링되는 건 아님
• minimal estimator variance : sub-optimal pdf는 가능한 최적의 경우와 가까워야한다.

 

 

3. 다른 알고리즘과 비교

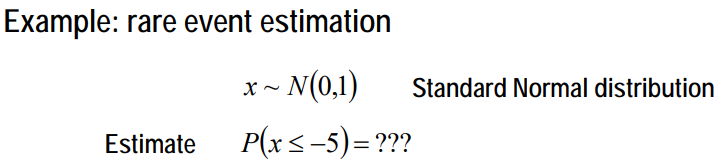
Random sampling 또는 LHS로 이 확률을 추정하려면 ~1억 개의 샘플링 포인트가 필요하다.

 

4. Python code

1) f(x)와 샘플 분포 p(x), q(x) 정의

def f_x(x):
    return 1/(1 + np.exp(-x))
    
def distribution(mu=0, sigma=1):
    # return probability given a value
    distribution = stats.norm(mu, sigma)
    return distribution
    
# pre-setting
n = 5000

mu_target = 3.5
sigma_target = 1
mu_appro = 1
sigma_appro = 1

p_x = distribution(mu_target, sigma_target)
q_x = distribution(mu_appro, sigma_appro)

 

2) p(x) 분포에서 샘플링한 실제 값 계산

s = 0
for i in range(n):
    # draw a sample
    x_i = np.random.normal(mu_target, sigma_target)
    s += f_x(x_i)
print("simulate value", s/n)

 

3) q(x)에서의 샘플과 어떻게 수행하는 지 살펴보자

value_list = []
for i in range(n):
    # sample from different distribution
    x_i = np.random.normal(mu_appro, sigma_appro)
    value = f_x(x_i)*(p_x.pdf(x_i) / q_x.pdf(x_i))
    
    value_list.append(value)

 

[참고 자료]

1. PowerPoint Presentation (cmu.edu)

2. [머신 러닝] 중요도 샘플링 (Importance Sampling)과 기댓값 추정 (tistory.com)

3. vol1lab16montecarlo2-pdf (byu.edu)